The RSA Algorithm

Developed in 1977 by Ron Rivest, Adi Shamir, and Len Adleman at MIT and first published in 1978
Rivest-Shamir-Adleman (RSA)
The most widely accepted and implemented general-purpose approach to public-key encryption
RSA scheme is a block cipher in which plaintext and ciphertext are integers between 0 and n-1 for some n
A typical size for n is 1024 bits, or 309 decimal digits
That is, n is less than 2^1024
RSA makes use of an expression with exponentials
Plaintext is encrypted in blocks, with each block having a binary value less than some number n
i.e. the block size must be less than or equal to log2(n) + 1;
In practice, the block size is i bits, where 2i < n ≤ 2i+1
For some plaintext block M and ciphertext block C, encryption and decryption are of the following form:

C = M^e mod n

M = Cd mod n = (M^e)^d mod n = M^ed mod n

Both sender and receiver must know the value of n
The sender knows the value of e, and only the receiver knows the value of d
This is a public-key encryption algorithm with a public key of PU = {e, n} and a private key of PR = {d, n}
For this algorithm to be satisfactory for public-key encryption, the following requirements must be met:

It is possible to find values of e, d, n such that M^ed mod n = M……… for all M < n.
It is relatively easy to calculate M^e mod n and C^d mod n for all values of M < n.
It is infeasible to determine d given e and n

By the first requirement, we need to find a relationship of the form M^ed mod n = M
This is equivalent to saying,

ed ≡ 1 mod φ(n)

d ≡ e-1 mod φ(n)

e and d are multiplicative inverses mod φ(n)
According to the rules of modular arithmetic, this is true only if d is relatively prime to φ(n)
Equivalently, gcd(f(n), d) = 1
We are now ready to state the RSA scheme. The ingredients are the following:

p, q, two prime numbers (private, chosen)

n = pq (public, calculated)

e, with gcd(f(n), e) = 1; 1 < e < f(n) (public, chosen)

d ≡ e-1 (mod f(n)) (private, calculated)

The private key consists of {d, n} and the public key consists of {e, n}
Suppose that user A has published its public key and that user B wishes to send the message M to A
Then B calculates C = Me mod n and transmits C
On receipt of this ciphertext, user A decrypts by calculating M = Cd mod n
The figure ahead summarizes the RSA algorithm
It corresponds to Figure a of Encryption with public Key: Alice generates a public/private key pair; Bob encrypts using Alice’s public key; and Alice decrypts using her private key

Figure: The RSA algorithm.

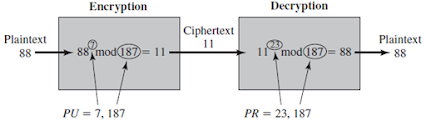
An example of RSA algorithm.

88^7 mod 187 = [(88^4 mod 187) × (88^2 mod 187) × (88^1 mod 187)] mod 187

88^1 mod 187 = 88

88^2 mod 187 = 7744 mod 187 = 77

88^4 mod 187 = 59,969,536 mod 187 = 132

88^7 mod 187 = (88 × 77 × 132) mod 187 = 894,432 mod 187 = 11

Let us look at an example, which shows the use of RSA to process multiple blocks of data
Here the plaintext is an alphanumeric string
Each plaintext symbol is assigned a unique code of two decimal digits (e.g., a = 00, A = 26)
A plaintext block consists of four decimal digits, or two alphanumeric characters
Figure ahead illustrates the sequence of events for the encryption of multiple blocks (a specific example)
The circled numbers indicate the order in which operations are performed

Figure: RSA approach with example.

Computational Aspects

Let's move towards the issue of the complexity of the computation in the use of RSA
Two issues to consider: encryption/decryption and key generation

For more details download the presentation given below:

References:

Cryptography and Network Security Principles and Practices, Fourth Edition By William Stallings.

Key Terms of Information Security